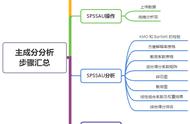
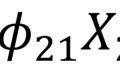PCA的本质：寻找几个线性组合将样本参数进行综合，从而更好的区分样本个体。

简单类比：对于学生成绩，每一科成绩有高有低，只看单科成绩很难区分，如果通过总成绩来判断那就容易多了。那么总成绩就是各科成绩的线性组合（综合），每科成绩权重都是相同的。

这其实就相当一个简单的主成分分析。只不过只有一个主成分。他的线性组合（综合）是算数平均值。

如果重视理科，就让数理化成绩的权重变大在求总成绩（综合），那么原来总分相同偏理科的总成绩就靠前了。如果把这类比为第二主成分。

横轴是总成绩，纵轴是理科权重加大的总成绩。这样就能把学生分成：总成绩好理科好，总成绩好理科差，总成绩差理科好，总成绩差理科差。

这样主成分分析就容易理解了。

主成分分析就是在寻找几个（一般是2个，不能太多否则意义不大）不相关的线性组合（重复相似组合没有意义），对样本参数综合，以便于最大程度区分样本个体。

本来要看6科成绩且不好区分，现在只看总成绩就能排序，成绩从6变成1就是降维，能够排序就是可区分即达到判别的目的。

变量的算术平均不改变总方差，因为变量权重都是1，总成绩方差=每科成绩协方差矩阵元素的和。方差即信息即差异即区分，如果没有差异就证明同质。所以不改变信息。

但是我们想要的不仅是总的方差不改变，同样需要能够更加的区分（所有的线性组合不相关），即对角线元素和=总方差且降序排序，非对角线元素尽可能接近0。这才是我们想要的线性组合。

这样可能需要的线性组合就会非常多，达不到降维的目的。所以只选取对角线元素的和接近原来80%以上就行。这样可能只需要少量的几个线性变换，但同时保留了80%的信息。

但是

协方差矩阵式是实对称矩阵。

实对称矩阵一定可以可对角化，即通过不相关的线性变换实现只有对角线有非0元素。

线性变换即特征向量。

对角线元素即特征值，其和=原方差。

所以这个问题就演化成：求协方差矩阵的特征对【特征值，对应的特征向量】

依次找最大的特征值（满足不低于原方差80%）及对应的特征向量即想要的线性变化。

最大特征值对应特征向量就是第一主城成分。

特征对呢，EXCEL也不是不能求，但是效率太低了。除非用代码这一个，或者自己手动算几天[捂脸][捂脸][捂脸]

使用Python对相关系数矩阵（或者协方差矩阵）进行求特征对（特征值，特征向量）numpy的np.linalg.eig(arr)函数直接求出

特征值：

特征向量：

协方差矩阵和相关系数的特征对是不一致的，但是重在理解，用哪个都行。

很明显最大的特征是第一个3.389和第二个1.390，这2个之和占整体在79.65%接近80%。那么对应的特征向量矩阵前两列就还是想要的线性组合。

再用R验证一下

第一个特征向量，权重基本都差不多且同方向，可以理解赋予总成绩的意义。

第二个特征向量，有正有负，可以理解赋予偏科情况的意义。

这样通过2个线性变换对参数进行综合，还能赋予其实际意义，区分也更加直观。