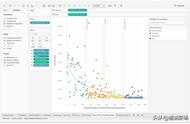
从上图可以看出，将3个班级的成绩进行方差齐检验，不同班级样本对于成绩全部均不会表现出显著性(p=0.442>0.05)，意味着不同班级样本数据的波动性均呈现出一致性，并没有差异性，通过方差齐检验，满足使用方差分析前提要求。

综上所述，样本数据通过了独立性检验、正态性检验和方差齐检验，满足方法分析的3个前提条件，可以使用单因素方差分析进行3个班级成绩的差异性研究。

4.非参数检验

但是，很多情况下，如果不满足方差分析的前提条件，则可以改用非参数检验进行分析。非参数检验不需要假定总体分布形式，直接对数据的分布进行检验。非参数秩和检验研究X不同组别时Y的差异性，针对方差不齐，或者非正态性数据（Y）进行差异性对比。

在本例中，使用SPSSAU的非参数检验进行3个班级成绩的差异性分析，分析结果如下图：

从上图可以看出，利用非参数检验去研究班级对于成绩的差异性，不同班级样本对于成绩全部均呈现出显著性(p<0.05)，意味着不同班级样本对于成绩均有着差异性。

数据满足3个前提条件，故使用SPSSAU单因素方差分析进行3个班级成绩差异性研究分析，分析结果如下图：

从上图可以看出，对3个班级成绩进行单因素方差分析，不同班级成绩均呈现出显著性差异（p<0.01）。具体差异可以通过比较成绩平均值得到，1班平均成绩为80.50分，2班平均成绩为71.37分，3班平均成绩为54.87分，差异明显。SPSSAU同时输出可视化图形进行直观对比，可通过折线图进行更加直观的对比，如下图：

从这次期末考试的成绩看，3个班级的成绩满足方差分析的前提条件，进行单因素方差分析研究3个班级成绩的差异性，得到如下结论：1班的平均成绩为80.5远远高于2班和3班，2班的平均成绩为71.37远远高于3班。3个班级的成绩差距过大，说明成绩好的同学基本集中在1班，成绩较差的同学基本集中在3班，不合理的班级结构，不利于学生的全面发展，学校应该进行重新分班的调整。