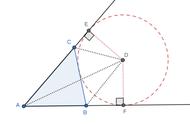
如图所示

结论：AB AC=BD CD.

角平分线模型

模型1 角平分线上的点向两边作垂线

条件：如图，P是∠MON的平分线上一点，过点F作PA⊥OM于点A, PB⊥ON于点B.

结论：PB=PA.

小结：利用角平分线的性质：角平分线上的点到角两边的距离相等，构造模型，为边相等、角相等、三角形全等创造更多的条件，进而可以快速找到解题的突破口.

模型2 截取构造对称全等

条件：如图，P是∠MON的平分线上一点，点A是射线OM上任意一点，在ON上截取OB=OA，连接PB.

结论：△OPB≅△OPA.

小结：利用角平分线图形的对称性，在角的两边构造对称全等三角，可以得到对应边、对应角相等.利用对称性把一些线段或角进行转移，这是经常使用的一种解题技巧.

模型3 角平分线 垂线构造等腰三角形

条件：如图，P是∠MON的平分线上一点，AP⊥OP于P点,延长AP交ON于点B.

结论：△AOB是等腰三角形.

小结：构造此模型可以利用等腰三角形的“三线合一”，也可以得到两个全等的直角三角形，进

而得到对应边、对应角相等.这个模型巧妙地把角平分线和三线合一联系在一起.

模型4 角平分线 平行线=等腰三角形