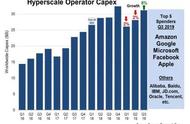
解析:显然,第一行(最上边一行)和第一列(最左边一列)中的数是相同的,在这一行(列)中,从第2个数起,每一个数与前面相邻的一个数相差3,例如7-4=10-7=13-10=16-13=…=3;第二行(列)中,从第2个数起,每一个数与前面相邻的一个数相差5;第三行(列)相差7;第四行(列)相差9;第五行(列)相差11.
在这个数表中,随便找一个自然数M,那么2M 1一定不是质数.例如,M=
4,2M 1=2×4 1=9,9不是质数;M=17,2×17 1=35,35也不是质数.而这个数表中没有的自然数M,则2M 1一定是质数.比如,M=5不在数表中,2×5 1=11,11是质数,M=8,2×8 1=17,17也是质数
6. (青少年国际城市邀请赛试题)若一个质数的各位数码经任意排列后仍然是质数,则称它是一个"绝对质数"。
例如2,3,5,7,11,13(31),17(71),37(73),79(97),113(131,311),199(919,991),337(373,733)…都是绝对质数.求证:绝对质数的各位数码不能同时出现数码1,3,7与9.
解析:正难则反。假设一个绝对质数同时含有数字1,3,7,9,由此导出矛盾,这是解题的关键,一个绝对质数如果同时含有数字1,3,7,9,则在这个质数的十进制表示中,不可能含有数字0,2,4,5,6,8,否则,通过适当排列后,这个数能被2或5整除。设N是一个同时含有数字1,3,7,9的绝对质数.

其中一定有一个能被7整除,这个数就不是质数,矛盾.
故原假设不成立,即绝对质数的各位数码不能同时出现数码1,3,7,9.

质数也好,合数也罢,反正都是自然数。其实合数也挺不容易的,即使是相邻的两个数字,距离再近,总是有先后吧,看似好像紧紧地贴在了一起,但是你就是你,独一无二,既与众不同,又孤独无依。将数学和哲学实现完美结合的古希腊人,视数学为哲学之起点,我不懂当前学问高深的数学,但是,双手赞同数学本来的含义:即学习、学问、科学之意。然而今天,数学已经成为一门抽象的学科,数学孤独了,一门学科尚且如此,更何况一个质数呢?所以孤独是注定的。
,