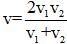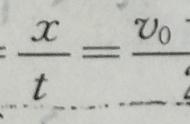滑动查看本书目录

（一）

法原部

法原部第一种为《平三角举要》，又名《三角法举要》，专论平面三角形，是中国历史上第一部三角学教程。书凡五卷，卷一《测算名义》，介绍点线面体、三角八线、比例等各种定义；卷二《算例》，阐述勾股、锐角、钝角三角形各项性质；卷三《内容》，讨论三角求积、内容方边、内容圆径、外接圆径求法；卷四《或问》，利用勾股定理证明三角各项性质；卷五《测量》，讨论测高、测远、测斜坡、测深等各种类型的三角测量方法。

（以下线图均取自本书）

第二种为《勾股阐微》四卷，专论勾股问题。卷一为杨作枚《勾股正义》，论勾股定理、勾股和较等基本勾股问题。卷二至卷四为梅文鼎原稿。卷二为勾股和较问题，附鲍燕翼勾股容方、分角线至对边等法。卷三为梅文鼎旧稿《用勾股法解几何原本之根》，利用勾股定理证明《几何原本》中若干问题，提出“几何不言勾股，然其理并勾股”。卷四为辑录梅文鼎《几何增解》《勾股测量》及其他勾股散稿汇编而成。

第三至第五种为梅文鼎论球面三角形三书，分别为《弧三角举要》五卷、《环中黍尺》六卷、《堑堵测量》二卷。《弧三角举要》是中国历史上第一部球面三角学教科书。书凡五卷，卷一《弧三角体势》，介绍球面三角基本性质及其分类；卷二《正弧三角形》，解球面直角三角形，论正弦定理；卷三《垂弧法》，讨论将一般球面三角形化为球面直角三角形求解之法；卷四《次形法》，讨论利用球面三角形边角对称、互余、互补构造新的球面三角形来求解的方法；卷五《八线相当法》，讨论三角八线比例关系，排列出四类二十一组成比例的三角公式。