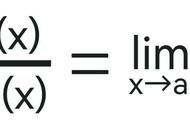或者

那么就有:

在区间的另一个端点也存在相类似的结果。这个定理就称之为洛必达法则,能有效地应用于待定型的极限计算。
3.不等式柯西中值定理在不等式的证明也有广泛应用,关键是f(x)和g(x)要选得恰当。
例2
试证明当x>0时,1 x ln(x √1 x²)>√1 x²。
证明:设

则f(t)和g(t)在区间[0,x]上满足柯西中值定理条件,所以存在ξ∈(0,x),使

来源:原点资讯(www.yd166.com)时间:2022-11-03 01:48:36作者:YD166手机阅读>>
或者

那么就有:

在区间的另一个端点也存在相类似的结果。这个定理就称之为洛必达法则,能有效地应用于待定型的极限计算。
3.不等式柯西中值定理在不等式的证明也有广泛应用,关键是f(x)和g(x)要选得恰当。
例2
试证明当x>0时,1 x ln(x √1 x²)>√1 x²。
证明:设

则f(t)和g(t)在区间[0,x]上满足柯西中值定理条件,所以存在ξ∈(0,x),使

(可加威信:yanxinlaoshi,获取更多考研资讯)距离考研初试只有短暂的一个月了,相信各位研友都在全力的冲刺复习中...
2022-11-03 01:53:59查看全文 >>
柯西中值定理本身并不难,用老黄自己的话说,就是:如果有两个函数在一个闭区间[a,b]上都可导,那么在对应的开区间(a,b...
2022-11-03 02:03:41查看全文 >>
本文主要是介绍柯西中值定理推导x→a时0/0型的洛必达法则的思路。柯西中值定理:如果函数f(x)及F(x)满足(1)在闭...
2022-11-03 02:14:01查看全文 >>
床头没有床头柜,生活起来多不方便,谁用谁知道!但是如果说,床头过道空间不够宽敞,可能只能摆放一个,或者连一个床头柜都摆不...
2022-11-03 01:42:17查看全文 >>
几乎家家都有过道,其实这里也可以有一定的装饰。今天看一下实例,可以借鉴一下。▲功能兼顾装饰,也就是朝向过道做收纳型柜子,...
2022-11-03 02:05:53查看全文 >>
如果你读过大学,那么很有可能学过高等数学,对下面几个定理应该有印象吧。罗尔定理:如果函数f(x)满足(1)在闭区间[a,...
2022-11-03 02:11:25查看全文 >>
拉格朗日中值定理(Lagrange Mean Value Theorem,提出时间1797年)又称拉氏定理,又称微分中值...
2022-11-03 01:25:27查看全文 >>
柯西定理定义我们同样进行拆解:柯西定理需要满足三个条件f(x),g(x)在[a,b]内连续f(x),g(x)在(a,b)...
2022-11-03 01:53:36查看全文 >>
拉格朗日中值定理(Lagrange Mean Value Theorem,提出时间1797年)又称拉氏定理,又称微分中值...
2022-11-03 01:46:42查看全文 >>
今天和大家回顾一下高数当中的微分中值定理,据说是很多高数公式的基础。由于本人才疏学浅,所以对于这点没有太深的认识。但是提...
2022-11-03 01:24:45查看全文 >>