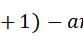我们同样进行拆解：柯西定理需要满足三个条件

• f(x),g(x)在[a,b]内连续
• f(x),g(x)在(a,b)内可导
• g'(x)不等于0

其中最后一个条件，可以推出以下式子成立：

对于第二个式子，很明显成立，那么我们看看第一个式子的推导（反证法）

假设g(a)=g(b),那么g(x)满足罗尔定理所需条件，那么我们可以得出结论：

综上所述，当满足上述三个条件时，可使用柯西定理。

这里的辅助函数我们可以参考上篇拉格朗日定理证明所设的辅助函数，证明如下：

对比罗尔定理，拉格朗日定理和柯西定理，我们可以发现一个特点：

• 罗尔定理是特殊的拉格朗日定理（或在特殊情况下的）
• 拉格朗日定理是特殊的柯西定理（或在特殊情况下的）

三大中值定理需要注意的是它们所需要的条件。