证明ab+cd=ef(其中a、b、c、d、e、f为图中已知的线段)几何题历来是中学数学学习中难点,面对这类问题一开始就令人觉得无从下手,或思考不了几步便黔驴技穷,最终都不得不遗憾地放弃.
笔者通过对这类问题的探索,发现这类的证明大多遵循着这样的思路:在线段e上找到一个点X,把该线段分为两条m、n,使其中的一条m满足ab=mf,然后再证明另一条n满足cd=nf,此时再把两式相加便有ab+cd=mf+nf=(m+n)f=ef.
这种解法跟代数中列方程解应用题的"设元"有点类似,姑且称之为——设未知点法.
具体请看以下几例.
例1 如图1,AB是半圆的直径,弦AC、BD相交于点E.
求证:AE·AC BE·BD=AB^2.

证明:设X是AB上一个点,则
=AB(AX BX)=AB·AX AB·BX,
令点X满足:AE·AC= AB·AX…………(1)
即AE/AB=AX/AC.
连接BC.
因为∠EAX=∠BAC,
所以ΔAXE∽ΔACB,
所以∠AXE=∠C,
因为AB为直径,所以∠C=90°,
所以∠AXE=90°,
所以∠BXE=90°.
连接AD.则∠D=90°,
因为∠EBX=∠ABD,
所以ΔBEX∽ΔBAD,
所以BE/BA=BX/BD,
所以BE·BD=BX·AB………………(2)
(1) (2),得:
AE·AC BE·BD=AB·AX BX·BA
=AB·(AX BX)=AB·AB=AB^2,
即AE·AC BE·BD=AB^2.
例2 如图2,ABCD是圆内接四边形.
求证:AB·CD AD·BC=AC·BD(托勒密定理).

证明:在AC上取点X,使
AB·CD=AX·BD…………(1)
连接BX,则在ΔABX与ΔDBC中,
AB/AX=BD/CD,
因为∠BAX=∠BDC,
所以ΔABX∽ΔDBC,
所以∠ABX=∠DBC,
所以∠ABX-∠DBX=∠DBC-∠DBX,
即∠ABD=∠CBX,
又∠ADB=∠BCX,
所以ΔABD∽ΔXBC,
所以AD/XC=BD/BC,
所以AD·BC=XC·BD…………(2),
(1) (2),得
AB·CD AD·BC=(AX XC)·BD=AC·BD.
例3 如图3,等腰ΔABC中,AB=AC,D是底边BC上任一点.
求证:AB^2=AD^2 BD·DC.

证明:在AB上取点X,使
AD^2=AX·AB………(1)
则AD/AX=AB/AD,
在ΔADX与ΔABD中,
因为∠BAD=∠DAX,
所以ΔADX∽ΔABD,
所以∠ADX=∠B,
因为AB=AC,
所以∠B=∠C,
所以∠ADX=∠C,
因为∠BDA=∠C ∠CAD,
即∠BDX ∠ADX=∠C ∠CAD,
所以∠BDX=∠CAD,
所以ΔDBX∽ΔACD,
所以BD/AC=BX/CD,
所以BD·DC=BX·AC……………(2)
(1) (2),得
AD^2 BD·DC =AX·AB BX·AB
=(AX BX)·AB=AB·AB= AB^2.
所以AB^2=AD^2 BD·DC.
例4(2013年全国初中数学联赛题)如图4,圆内接四边形ABCD中,CB=CD.
求证:CA^2-CB^2=AB·AD.

证明:把求证式改为
CA^2=CB^2 AB·AD.
在CA上取点X,使
CB^2=CX·CA………(1)
连接BX.则在ΔCBX与ΔCAB中,
CB/CX=CA/CB,
因为∠BCX=∠ACB,
所以ΔCBX∽ΔCAB,
所以∠CXB=∠CBA,
因为四边形ABCD内接于圆,
所以∠CBA ∠D=180°,
所以∠CXB ∠D=180°,
因为∠AXB ∠CXB=180°,
所以∠AXB=∠D,
因为CB=CD,
所以∠XAB=∠DAC,
所以ΔABX∽ΔACD,
所以AB/AC=AX/AD,
所以AB·AD =AX·CA………………(2)
(1) (2),得
CB^2 AB·AD=CX·CA AX·CA
=CA(CX AX)=CA·CA= CB^2,
所以CA^2-CB^2=AB·AD.
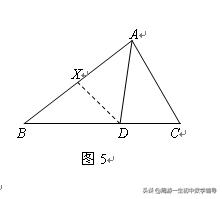
例5 如图5,AD为△ABC的角平分线,
求证:AD^2=AB·AC-BD·DC.
证明:把求证式化为:
AD^2+BD·DC=AB·AC.
在AB上取点X,使
AD^2=AX·AC…………(1)
连接DX,则在△ADX与△ACD中,
AD/AC=AX/AD,
因为AD为△ABC的角平分线,
所以∠DAX=∠DAC,
所以ΔADX∽ΔACD,
所以∠AXD=∠ADC,∠ADX=∠C,
因为∠BXD ∠AXD=180°,
所以∠BXD ∠ADC=180°
所以sin∠BXD=sin∠ADC;
因为∠BDA=∠C ∠CAD,
即∠BDX ∠ADX=∠C ∠CAD,
所以∠BDX=∠CAD,
所以sin∠BDX=sin∠CAD.
在△BDX与△ACD中,分别由正弦定理,得:
BD/BX=sin∠BXD/sin∠ADC,
AC/DC= sin∠BDX/sin∠CAD,
所以BD/BX=AC/DC,
所以BD·DC=BX·AC………………(2)
(1) (2),得
AD^2 BD·DC= AX·AC BX·AC
=(AX BX)·AC
=AB·AC,
所以AD^2=AB·AC-BD·DC.
从以上各例的证明来看,这种设未知点法的思路与运用过程可用口诀归纳为如下口诀:
取点得到等积式,化为比例证相似,相似推出角相等,再把相似比例证,化等积再相加,整理即把结论证。
,