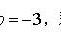函数 y = x * ln(x) 的图像是一个连续的曲线,它在 x 轴上从原点开始,随着 x 的增大逐渐向上弯曲。当 x 接近 0 时,函数的值趋近于负无穷大。随着 x 的增大,函数的值也增大,但增速逐渐减慢。当 x 趋近于正无穷大时,函数的值趋近于正无穷大。这个函数在 x > 0 的范围内是单调递增的。整个图像在 x 轴的右侧,没有定义在 x 轴的左侧。
∵lim(x→1)ⅹlnx=lim(x→1)lnx/1/x
=lim(x→1)1/x/(-1/x²)=-1
lim(ⅹ→0+)xlnx=lim(x→0+ )lnx/1/x
=lim(ⅹ→0+)1/x/(-1/x²)=lim(x→0+)(-ⅹ)
=0
所以图像经过原点(0,0),和点(1,-1),在x∈(0,1]内为降函数,在x∈(1,+∞)时图像为在第一象限但不包括点(1,0)单调递增的曲线。