Kenneth G. Wilson（1936 6 .8—2013 6 .8）美国物理学家。因建立相变的临界现象理论，即重正化群变换理论，获得了1982年度诺贝尔物理学奖。

Wilson 认为：相变的临界现象与物理学其他现象不同的地方在于，人们必须在相当宽广的尺度上与系统中的涨落打交道。所有尺度上的涨落在临界点都是重要的，因此，在进行理论描述时，要考虑到整个涨落谱。威尔逊的临界现象理论是在重正化群变换理论的基础上作了实质性的修改后建立的。威尔逊的临界现象理论，全面阐述了物质接近于临界点的变化情况，还提供了这些临界量的数值计算方法。

重整化群是一个在不同长度标度下考察物理系统变化的数学工具。

标度上的变化称为“标度变换”。重整化群与“标度不变性”和“共形不变性”的关系较为紧密。共形不变性包含了标度变换，它们都与自相似有关。在重整化理论中，系统在某一个标度上自相似于一个更小的标度，但描述它们组成的参量值不相同。系统的组成可以是原子，基本粒子，自旋等。系统的变量是以系统组成之间的相互作用来描述。

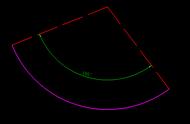
可以看一下下面的图片。所谓粗粒化，就是在干和下图类似这种事情，从上到下像素在降低，也就是标尺在增大。

对于具有自相似性的系统，我们在不同的标度 （即不同的标尺刻度）下对其进行观察时，会发现这种系统具有所谓的“标度不变性" 。从上图可以看到， 图片从a到d的过程标尺在扩大，d与a相比一些细节被平均掉了，但d与a有着相似的结构，图像的基本特征是完全相同的。" 这意味着在不同的标度下，系统表现出的物理行为本质上相同" 这一性质就叫做标度不变性" 。

标度不变性对应着一种对称性，描述对称性的工具是群论。粗粒化过程丢失了一部分信息，因此这种操作是不可逆的，所以重整化群是一种半群。

在我看来，需要重整化的理论，一定有我们没有看到的地方。就是我们找到为什么该理论要重整化才合理的根本原因。

但重整化和重整化群的概念非常好，因为我们在探索宇宙的规律的过程中，必然不能把握所有。所以尤其是重整化群在处理系统边界问题的时候，给我们了一个有力的工具。也便于我们理解非线性波动。

这个理论在将来必须广泛用到，而且对于找爱氏场方程解，杨——米尔斯理论解都非常重要。这就是我的观点。

最后的这一点内容，内容不多，但意义非凡，大家一定多去领会。