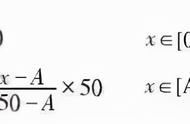六年级的小可爱们，第六单元《百分数（一）》已经上完或者差不多上完了吧，也就意味着月考或者单元测试马上就要进行啦。

一起复习一下百分数这一单元的知识点和必考题型吧，本文最后还附带了一张长图，总结了本单元要点，各位家长和同学可以收藏或保存备用。

1、百分数的意义：表示一个数是另一个数的百分之几的数叫做百分数，也叫做百分率或者百分比。

【概念对比】分数的意义：把单位“1”平均分成若干份，表示其中的一份或几份的数就是分数。

2、百分数的读法和写法：百分数通常不写成分数的形式，而是在分子后面直接加上百分号“%”，读作“百分之……”。

3、分数和百分数的联系和区别：

• 分数既可以表示一个具体的数字（带单位），又可以表示两个数之间的倍数关系（不带单位），如一根绳子长3/5米，苹果的数量是梨的2/3；
• 百分数只能表示两个数之间的倍数关系（不带单位），不能表示一个具体的数值，因此百分数是不能带单位的；
• 分数可以约分化简，假分数可以写成带分数的形式；但百分数不能约分，也不能写成带分数的形式，假分数的分母固定是100，并且要写成“%”的形式；
• 分数的计算结果需要化简到最简分数，分子和分母只能是整数；百分数的分母固定是100，分子可以是整数，也可以是小数。
• 百分数和分数是100的分数的意义是有区别的，如47/100和47%在数字大小是相等的，但二者的意义不一样。

4、百分数和小数之间的相互转化：

百分数化为小数：小数点向左移动两位，再去掉百分号即可；

小数化为百分数：小数点向右移动两位，再加上百分数即可。

5、百分数和分数之间的相互转化：

百分数化为分数：把百分数写成分母是100的分数，再把这个分数约分化简到最简分数即可；

分数化为百分数：用分数的分子除以分母使之化为小数，再将小数点向右移动两位，加上百分数即可。（当分数的分母是100的因数或者倍数的时候，也可以直接用分数的基本性质，使其变成分母是100的分数，再写成百分数的形式。）

注意：除不尽的时候通常保留3位小数，也就是百分号前保留一位小数。

6、常见的百分率及其计算方法：日常生活中常见的、考试常考的百分率包括学生的出勤率、考试的及格率、产品的合格率、小麦的出粉率、花生的出油率、树苗的成活率等等。

这类百分率本质上都是指部分占总体的百分之几，如出勤率指出勤人数占总人数的百分之几、成活率表示成活的树苗占树苗总数的百分之几。其共同特点是分子≤分母，也就是这类百分率≤100%，最大取值就是100%，不可能超过100%。

还有另外一类百分率，如销量的增长率、工厂的增产率、商店的利润率等，这类百分率涉及到的两个数之间有明显的前后顺序或时间的先后顺序，如今年和去年产量相对、本月和上月产量相比、现价和原价相比等，其分子是有可能大于分母的，所以增长率、增产率、利润率是有可能大于100%。

7、百分数解决实际问题

• 求一个数是另一个数的百分之几：一个数÷另一个数，结果化为百分数即可。
• 求一个数比另一个数多（少）百分之几：两数差÷另一个数，结果化为百分数即可。
• 求一个数的百分之几是多少：一个数×百分之几，也就是单位“1”×百分率=部分量。
• 求比一个数多（少）百分之几的数是多少：单位“1”×（1 百分率）=部分量、单位“1”×（1-百分率）=部分量。
• 求一个数两次增减变化之后的变化幅度：1×（1 增加幅度）×（1-减少幅度）。如一个书包先降价10%，再提价10%销售，实际价格和原件相比是高了还是低了？设原价为1，1×（1-10%）×（1 10%）=99%，也就是最后的实际价格是原价的99%，比原价低了1%。
  

实际上，百分数解决问题的解题思路和分数乘除法的量率对应解题思路是一模一样的，实际上百分数也经常与分数应用题结合在一起考察。需要回头复习的同学戳这里：

百分数这一单元的单元测试卷一会就发出来，复习完的同学顺带就可以把测试卷完成了！

​