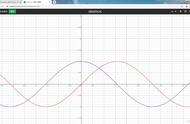
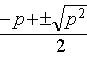有学生问到了凸凹反转在导数中的应用，今天就此做一个简述。

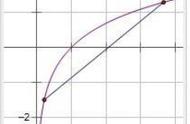
函数的凸凹性其实就是看在某一区间内二阶导数的保号性，凸凹性发生改变的点叫拐点，但在导数中的凸凹性并非一定是严格凸凹的，只需函数不单调，在区间内存在极大值或极小值，即有一个容易确定的极值(或最值)即可。

凸凹翻转的使用场景肯定和指对数同时存在的函数有关，常用于指对数混合函数的证明中，也可以用在恒成立求参数范围的题目中，若求参这种方法并不建议使用，其实凸凹翻转还可适用于根据函数个数求参数范围的题目中或根据指对数有无交点扩展出的恒成立求参问题，这里不得不又搬出那个经典的题目，如下：

上述题目就是一个典型的根据凸凹性求参数范围的题目，由于题目较为简单，指对数的凸凹性很容易判断，但如果函数中指对数的形式较为复杂或添加了其他类型的函数，此时函数如何分组？如何确定凸凹性？如何确定可用凸凹反转解题？

至于如何分组这并没有太好的方法，以混合型函数的证明为例，指对数要放到不等式的两侧，证明f(x)min≥g(x)max，但指对数分别与不同的函数结合会产生不同的函数形态，结合之后的函数有无所需的极值最值，有无所需的凸凹性都不确定，指对数与哪些函数结合有两个判定方法，一是根据常见的指对数型本身的单调性和极值点情况，二是要会判断一些复杂函数的极限值，例如y=lnx-x，当x→-∞时，y→-∞；当x→ ∞时，lnx的增长速率要远小于x的增长速率，此时y→-∞,因此可初步判定函数的趋势为增减趋势，函数存在极大值点，可看作上凸函数，y=lnx-x²的趋势也类似，当然上述例子很简单，但极限是判断函数有无极值最有利的工具，因为不可能再像常规做法那样去求导判断单调性。

以上是六种最基本的指对数模型，函数的形态可结合在定义域端点和无穷处的极限值来辅助记忆，若基本模型与其他式子结合，可用不同函数的增长速率不同辅之以极限法确定，关于凸凹反转，以下面的题目为例：

本题证明方法有很多，若用凸凹反转来证明，左右各除x有两个考虑，一个这是对对数函数的常规处理(对数构加减)，二是从左右两侧函数的趋势考虑，至于为什么左右两侧各添加一个-x，是因为右侧lnx-x是一个常见存在极大值的函数形态，但若只从右侧形态出发还可以添加-x²，但次数越高，函数形态越复杂，一切从简，此时能确定右侧为上凸函数存在最大值，而左侧函数可用极限值来确定一下大致的趋势，分别计算在x=0和x= ∞处的函数值，函数最有可能的是单增或存在一个极小值(基于猜测而已)，再计算一下左侧的导数值加以判断即可。

从上题能看出，与指对数有关的证明题用凸凹反转来做很多时候就像摸着石头过河一样，心理着实没底，但除了凸凹反转，更多的时候是先对指对数函数预处理，构造函数求最值，此时可能会用隐零点法，或者直接通过放缩来证明。

以上用凸凹反转时对左右函数取得最值的x值并不要求，但若用该方法求参数范围，那么必须要求在同一点取得最值，这一点就很难预测，因此这也不作为指对数恒成立求参的主要方法，知道即可，相关的例子如下：