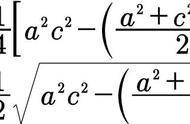这两个三角形是最常见的两个特殊三角形,从小学就已经开始接触,对于这两个三角形的三边关系必须熟记。

性质:
1、含30°角的直角三角形:长直角边是短直角边的√3倍,斜边是短直角边的2倍。
2、含45°角的等腰直角三角形:斜边是直角边的√2倍。
证明:
1、可由定理30°角所对直角边等于斜边的一半及勾股定理证明。
2、可由勾股定理证明。
技巧:实际计算中,先求最短边。
二、底角是30°的等腰三角形
性质:底是腰的√3倍。
证明:可分割为两个含30°角的直角三角形,利用含30°角的直角三角形的性质推导。
应用:常见于正六边形中。
三、黄金三角形(有一个角是36°的等腰三角形)
性质:短边/长边=(√5-1)/2
证明:利用相似及黄金分割即可证明。
应用:常见于正五边形中。
四、顶角是30°的等腰三角形
性质:短边/长边=(√6-√2)/2(可类比黄金分割比记忆)
证明:作腰上的高,由含30°角的直角三角形的性质及勾股定理可得。
应用:常见于正十二边形中。
五、等边三角形
性质:
证明:作高,分割为2个含30°角的直角三角形,由其性质及三角形面积公式可得。
小结熟练掌握常见的特殊三角形的性质,可缩短思考过程,加快解题速度。对于小题的速解以及大题的分析均有帮助。