在学习几何知识时，所有的形状都是完美的，没有公差的概念。基准也是完美的，只是由于现实中没有完美的东西，只要精度足够高，就当作完美的来看。

"解析几何"让我们知道，有了坐标系，就可以精确表述任何空间形状。基准就相当于坐标系，只是基准要从零件上得到。这个过程称为模拟（simulation），所用的高精度器具称为模拟器(simulator)，如机床工作台、平台等。

根据基准特征是形状、基准地位以及实体状态，具体模拟方法会有所不同。具体组合如表1所示。

表1. 基准特征和基准的组合关系

下面依次概述每种组合的模拟方法。

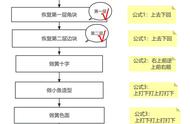
1. 平面作主基准：按一定的步骤，得到和零件的实际平面的高点形成接触的基准面。具体参见图1。对于任一个实际平面，能满足要求的基准面不止一个。选择其中任何一个都可以。

图1. 平面作为主基准时的模拟步骤

2. 圆柱体作主基准：这需要细分RFS, MMC, LMC三种情况。

2.1 圆柱体主基准RFS：所有实际配合包络面的轴线都可以。满足要求的包络面可能有多个。

2.2 圆柱体主基准MMC：直径等于MMC实效状态尺寸（对于内特征，为"最小孔尺寸-几何公差值"；对于外特征，为"最大轴尺寸 几何公差值"。MMC实效状态是从配合角度考虑问题。）的圆柱体模拟器的轴线。由于不限制模拟器的朝向和位置，因此可得到很多轴线。选择其中任何一个都可以。

2.3 圆柱体主基准LMC：直径等于LMC实效状态尺寸（对于内特征，为"最大孔尺寸 几何公差值"；对于外特征，为"最小轴尺寸-几何公差值"。LMC实效状态是从材料厚度角度考虑问题。）的圆柱体模拟器的轴线。由于不限制模拟器的朝向和位置，因此可得到很多轴线。选择其中任何一个都可以。

3. 宽度作主基准：比照"圆柱体主基准"处理，即也有RFS, MMC, LMC之区别，但需将圆柱体的"直径"替换成两平行面的"间距"，将"轴线"替换成"中间面"。

4. 球体作主基准：比照"圆柱体主基准"处理，即也有RFS, MMC, LMC之区别，但需将圆柱体的"直径"替换成球的"直径"，将"轴线"替换成"点"。

实效状态尺寸的计算公式见表2，但请注意表中均取半值（即算的是半径，不是直径；是平行面间距离的一半，不是全距离）。

表2. 基准特征和基准的组合关系