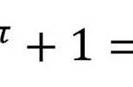好奇宝宝:
图中的那个加号“ ”是什么意思?
解答者:
嗯,我试图使用加号“ ”来说“这公式是真的”,类似的, 假定“¬”的意思是那个公式是假的。一个普通的想法是,我们现在有一个公式来检查3-圈,把它们与像0,1,2这样的标准数区分开来。
好奇宝宝:
我明白了。所以,通过添加¬∃x:x=SSSx作为一条新的公理,所有含有A,B,C或者任何其它的非标准数的3-圈的模型,我们就可以都去除了。
解答者:
是的。
好奇宝宝:
不过,这样向自然数的基础理论添加一条公理,好像过于随意。我的意思是,我从来没有看到过这样描述自然数的尝试:把“没有一个数等于它自己加3”作为一个基本的前提。看起来它应该是一条定理,而不是公理。
解答者:
那是因为它是通过引入一个更加一般的的规则来引入的。具体来说,一阶算术有一个无穷公理模式——一个无穷但是可计算的公理模式。这个模式的每一条公理说了,对于一个一阶公式Φ(x):
1. 如果Φ在0是真的,即Φ(0)
2. 只要Φ在一个数时为真,则在这个数的后继也为真,即∀x: Φ(x)→Φ(Sx)
3. 那么,Φ在所有数都是真的: ∀n: Φ(n),即
(Φ(0) ∧ (∀x: Φ(x) → Φ(Sx))) → (∀n: Φ(n))
换句话说,对于每一个公式,它在0时真的,它在每一个使它为真的下一个数都是真的,那么它在任何一个数都是真的。这就是一阶算术的归纳模式。作为一个特例,我们有这个归纳公理:
(0≠SSS0 ∧ (∀x: (x≠SSSx) → (Sx≠SSSSx)) → (∀n: n≠SSSn)
好奇宝宝:
不过那并没有说对于所有的n, n≠n 3。它给出了一些前提条件,然后根据这些前提能可以得出最后那个结论,但是我并不知道那些前提条件在哪里。
解答者:
啊,然而,使用算术的其它公理,我们证明那些前提条件,从而证明了这个结论。公式(SSSx=x)在0是假的,因为0不是任何数的后继,包括SS0。类似地,考虑公式SSSSx=Sx,我们可以整理为S(SSSx)=S(x)。如果两个数有相同的后继则它们是相等的,于是SSSx=x。根据逆否命题等价的逻辑规则:如果在Sx的真实性证明了在x的真实性,那么,在x为假就证明了在Sx为假。于是那个公式在0是假的,当它是假的时候它的后继也取值为假,于是根据一阶算术的归纳公理模式它必然处处为假。所以,一阶算术可以去掉像这样的模型:

好奇宝宝:
...嗯,我认为我明白了。如果这个模型遵守了我们已经指定了的其它公理(它们没有去除掉这个模型),比如“零不是任何数的后继”、“拥有同样后继的两个数相等”——那么我们可以证明公式x≠SSSx 在0是真的,可以证明那个公式如果在x是真的那么在x 1也是真的。所以,一旦我们更进一步地添加公理x≠SSSx在0是真的,以及如果x≠SSSx在y是真的则在Sy也是真的,那么x≠SSSx在所有的x都是真的...
解答者:
我们已经得到了这些前提条件了,所以我们得到了那个结论 ∀x: x≠SSSx,从而去除了所有的3-圈。对于任意的N,类似的逻辑可以去除N-圈。”
好奇宝宝:
所以,我们去除了所有的非标准自然数、只留下了标准自然数?
解答者:
不。因为还存在与-2*, -1*, 0*, 1* 这个无穷链相关的问题。

好奇宝宝:
这里有一个想法可以用来去除掉带有无穷链的模型。链中的所有非标准自然数都大于标准自然数,对吧?比如,如果w是一个非标准自然数,那么w>3, w>4,等等?
解答者:
我们可以归纳地证明没有一个数小于0,并且w不等于0、1、2、3、……,所以我必须同意那一点。
好奇宝宝:
OK.我们也能够证明:如果x>y,那么x z > y z.所以如果我们有一个非标准数w并且讨论w w, 那么w w一定大于w 3, w 4等等。
所以w w不能是哪个无穷链的任何部分,然后相加两个数应该产生第三个数。
解答者:
事实上,那就证明了,如果存在一个无穷链,那就必然存在两个无穷链。换句话说,图片里面最原始的那个模型,仅仅它自己是不能作为一阶算术的模型的。那个链蕴含着其它的元素,展示了这一点不意味着证明了那个链不存在。类似地,由于所有的数为奇数或者偶数,我们一定可以找到一个v使得v v = w 或者v v 1 = w。于是v必然是另一个非标准链的一部分,这个非标准链在那个含有w的标准链的前面。
好奇宝宝:
不过,那就要求有无穷多个无穷非标准数的链,这些非标准数都大于任何标准数。也许我们可以扩展这个逻辑,最终获得一个矛盾,从而一开始就去除无穷链 —— 比如,我们可以证明任何完备的非标准数的类必定大于它自己?
解答者:
想法很好,不过,并不可行。你将得到这样的结论:如果一个非标准数存在,它必定是一个双向无穷的链的一部分,这个链看起来像是负整数与正整数的有序拷贝。如果一个无穷链存在,那么存在对应于所有有理数的无穷多个链。所以呢,可以作为一阶算术的非标准模型的某个东西,必定至少含有标准数,紧接着一个有理数的拷贝(每一个有理数都被一个整数所代替)。然后,加法、乘法在这个设定中都走得通——我们不能证明它可能比我们已经说过的更大。”
好奇宝宝:
OK, 那么我们如何才能去除掉无穷多个无穷链的非标准自然数、仅仅保留开始的标准自然数呢?它们将违反什么样的陈述句——什么类型的公理才可以排除掉多余的数呢?
解答者:
为此,我们必须使用二阶逻辑。
好奇宝宝:
坦白地说,我不是100%地清楚它们的区别。
解答者:
OK...早先你给我一个可以检测出奇数的公式。
好奇宝宝:
是的。∃y: x=(2*y) 1,在x=1,x=9等等地方为真,不过在x=0为假。
解答者:
当你依据数的类来思考的时候,那就存在一些能够被公式所定义的类。例如,奇数 {1, 3, 5, 7, 9, ...}的类可以被这个带有自由变元x的公式所定义: ∃y: x=(2*y) 1。不过呢,你也可以试着去仅仅就类论类地讨论{1, 3, 5, 7, 9, ...}这个数集,是否存在一个定义了它的公式。
好奇宝宝:
等一下,如果你不能定义一个说明了某些东西是否是这个集合的元素的公式,你怎么能谈论一个一个集合呢?我的意思是,从理性主义者的视角来看,那样貌似感觉不爽。
解答者:
嗯...还记得先前关于小猫的谈话吗?

假定你像这样谈说,‘存在一个小猫的类,使得任何一只小猫只喜欢这个类中的其它小猫’。给我一个装满小猫的屋子,我可以计数出所有可能的类,对于每一个类检查你的陈述,这样就可以看到是否真的存在一个像那样说的类。所以那个陈述句是有意义的——它是可以被否定或者检查的,它限制了实在的状态。不过你并没有给我一个局部的公式以便我抓起一只小猫就能判断它是否在这个神秘的类之中。我必须遍历所有的小猫的类来寻找满足你的陈述句的类,只有到那时,我才能判断任何具体的单只小猫是否在那个类中。不过那个陈述句仍然有可错性,虽然使用数学的术语,它是非直谓的([译注1])——以下情况我们才能那样称呼它:当你构造了一个你只能通过考察很多可能的类来核实的陈述句,并没有从一个特殊的、你告诉了我如何构造的类来开始。
好奇宝宝:
啊... 嗯。如果是在有无穷只小猫的世界里,你不能在有限时间内遍历所有可能的类呢?
解答者:
如果你说,‘存在一个小猫的类,它们都互相喜欢’,我可以展示出来一个拥有三只小猫的彼此喜欢的类,于是就证明了那个陈述句是正确的。如果你说‘存在一个类,它有四只小猫,它们互相喜欢但不喜欢别的猫’,在已经知道小猫的其它特性的情况下,我也许可以提供一个构造性的证明来证明你的陈述是错的;每次,你给我四只猫,我可以找到第五只猫,它被你的四只猫的一只所喜欢,从而否定了你的努力。不过,这就把我们带到了关于数学的非常深入的部分了,我们暂时不去讲它。重点是即使是无穷的世界里,仍然存在二阶的陈述让你在有限时间内证明或证否。一旦你承认那些特殊的二阶陈述句是在有意义地说明一些东西,好吧,也许,你会承认一般的二阶陈述句也是有意义的。
好奇宝宝:
……对我来说那听起来有点怪怪的,也许不久以后我们会遇到麻烦。
解答者:
你不是唯一一个纠结这个的“数学家”。
好奇宝宝:
不过让我们回到自然数吧。你说我们可以使用二阶逻辑来去除任何的无穷链。
解答者:
是的。在二阶逻辑中,我们可以在一条陈述句中,直接对所有可能的类进行量化,而不必使用所有公式上的无穷的公理模式: