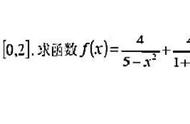当然，提到有趣的数学怎么会少了几何学呢？在中学，即便不喜欢数学的学生也会觉得不少几何题目趣味性非常强。关于几何学的一个真实的故事发生在2002年北京的国际数学家大会上，会上有个有趣的问题：任给一个五角星，对每个角上的三角形作外接圆，证明这个五个外接圆的交点共圆。据说，在场的世界最著名的数学家们无一能立即给出证明过程（看来，做中学数学题目还数中学的数学老师厉害）。传说，当时的大会主席吴文俊先生会后通过数学机械化方法利用计算机证明了该命题。

吴文俊是我国著名数学家，他在拓扑学方面做出了奠基性的工作，其研究成果被称为“吴公式”“吴示性类”“吴示嵌类”等。他通过汲取中国古代数学的精髓，尝试用计算机证明几何定理，开创了数学机械化的道路。他发明的数学机械化方法在国际上被誉为“吴方法”。该方法推动了自动推理的发展。吴先生还曾获得过国家最高科学技术奖。

吴文俊（1919-2017）与《几何定理机器证明的基本原理》

上面的小故事是关于平面几何的。在立体几何中，则充满了更多的奥秘。例如：正多面体是指一种特殊的凸多面体，它的每个面都是有相同边数的正多边形、每个顶点都是有相同棱数的端点。正多面体只有正四面、正六面、正八面、正十二面、正二十面体。可以证明，其它面数的正多面体是不存在的。

在三维空间的二维曲面，比如一张纸，具有正面与反面两个面。如果在正面有一只蚂蚁，只要它不从边界上翻到另外一面，它就永远在正面而爬不到反面。德国数学家、拓扑学的先驱莫比乌斯构造出了一个神奇的拓扑形状，他把一根纸条扭转了180°后再将两头拼接起来，就得到了著名的莫比乌斯带（环）。莫比乌斯带的神奇之处在于，它只有一个面。当一只蚂蚁从这个纸带的任意地方出发，沿着纸带的方向爬行，即可遍历这条纸带原先的两面。