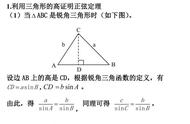
1.正弦定理

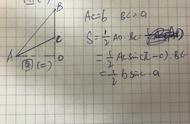
在一个三角形中，各边的长和它所对的角的正弦的比相等，即在△ABC中，

其中R为△ABC外接圆的半径

2.三角形内角关系式

（1）三角形内角和定理：A B C=π

（2）内角正弦关系：

sinA=sin（B C）

sinB=sin（A C）

sinC=sin（A B）

（3）内角余弦关系：

cosA=-cos（B C）

cosB=-cos（A C）

cosC=-cos（A B）

例：

1．在△ABC中，a＝3，b＝5，sinA＝，则sinB＝（　　）

A． B． C． D．1

【分析】由正弦定理列出关系式，将a，b及sinA的值代入即可求出sinB的值．

∴由正弦定理得：sinB＝=

故选：B．

【点评】此题考查了正弦定理，熟练掌握正弦定理是解本题的关键．

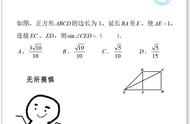
2．在△ABC中，AB＝，∠A＝75°，∠B＝45°，则AC＝　 　．

【分析】由三角形的内角和定理可得角C，再由正弦定理，计算即可得到AC．

【解答】解：∠A＝75°，∠B＝45°，

则∠C＝180°﹣75°﹣45°＝60°，

由正弦定理可得，=

即有AC＝=2

故答案为：2．

【点评】本题考查正弦定理的运用，同时考查三角形的内角和定理，考查运算能力，属于基础题．