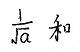两个公式都有注意点，公式一中要注意根号中的被开方数必须是非负数，这也是二次根式有意义的条件。公式二最容易出错，有两个易错点，其一：直接开根得到答案为a，这也是最常犯的错误；其二在去绝对值时，得到本身a认为a的取值范围是大于0，其实应该为大于等于0，得到相反数-a，a的取值范围应该小于等于0.

直接化简

在直接化简时，有些题目有隐含条件，需要我们自己去挖掘，有些题目没有隐含条件，就是简单的化简求值题，题目会默认被开方数大于等于0.

分析：本题中被开方数是分式的形式，需要化简，根据被开方数是非负数，可以得到1-a＞0，即a＜1。

在化简时，有两种方式，一种是把根号外的部分平方以后移入根号内，然后再进行化简。但是，在移动的过程中还要注意，括号外面的代数式a-1为负数。另外一种方法是将根号中的分式进行分母有理化，即分子、分母同乘以1-a，得到上述的平方再开根先变成绝对值，然后再进行化简。

将根式外的数或代数式移到根号里面时要是正数，不能随随便便就移进去，特别是代数式。

平方再开根一定要先变成绝对值，不要直接去根号，那样很容易出错。

条件化简

给定条件再化简，给定的条件可能是具体的范围，也可能多个字母之间的关系，也可能是数轴，变化多样，但是解题思路万变不离其宗。