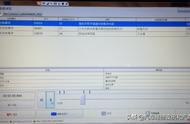
从上表可以看出，R方=0.973，说明自变量可以解释因变量97.3%的变化原因，模型拟合较好。当进行模型调整时，可以关注调整后R方的变化。

（4）模型公式

从上表可知，将工作经验,初始工资,教育程度作为自变量，而将工资作为因变量进行线性回归分析，从上表可以看出，模型公式为：工资=18473.846 145.782*工作经验 0.333*初始工资-274.265*教育程度

特别提示：构建回归模型使用非标准化回归系数，它是方程中不同自变量对应的原始回归系数，反映了在其他自变量不变的情况下，该自变量每变化一个单位对因变量作用的大小。通过非标准化回归系数构建的回归方程，才可以对因变量进行预测。

（5）自变量影响大小比较

从线性回归结果可以看出，工作经验、初始工资、教育程度的标准化回归系数分别是：0.8929、0.1536、-0.0463；所以工作经验对工资的影响最大，其次是初始工资，影响最小的是教育程度，且初始工资与工作经验对工资的影响是显著正向的，而教育程度对工资的影响是显著负向的。

特别提示：自变量对因变量影响大小的比较是通过标准化回归系数进行比较的。标准化回归系数的绝对值越大，说明该自变量对因变量的影响越大。标准化回归系数，是对自变量和因变量同时进行标准化处理后所得到的回归系数，数据经过标准化处理后消除了量纲、数量级等差异的影响，使得不同变量之间具有可比性。
本案例多元线性回归分析至此结束。

四、总结

总结一下多元线性回归分析的过程：

1、确定研究目的；多元线性回归分析用于研究哪些自变量会对因变量Y产生影响，得到回归方程，还可以通过方程进行预测，确定方法选择正确。

2、多元线性回归分析共有6个前提条件，满足后可进行分析，如果不满足需要对数据进行一定的修正，或者改用其他方法进行分析。

3、F检验用于判断模型总体显著性，显著说明模型有意义，可以继续进行后续分析。

4、t检验用于判断各个回归系数显著性，检验各自变量对因变量影响是否显著。

5、R方用于判断模型的拟合优度，通常越大越好。

6、构造多元线性回归模型使用非标准化回归系数，由此得到的回归模型才能用来预测。

7、比较自变量对因变量影响大小使用标准化回归系数，绝对值越大，影响越大。

,