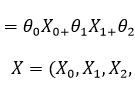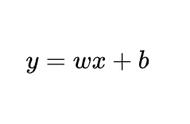，我们根据一次简单的二项分布实验，得到了一个关于 θ 的函数，这实际上是一个似然函数，根据不同的 θ 值绘制一条曲线，曲线就是θ的似然函数，y轴是这一现象出现的概率。

从图中可见，当 等于 0.7 时，该序列出现的概率是最大的，因此我们确定该硬币正面朝上的概率是0.7。

因此，回到正题，我们要求的是误差出现概率 的最大值，那就做很多次实验，对误差出现概率累乘，得出似然函数，带入不同的 ，看是多少时，出现的概率是最大的，即可确定的值。

综上，我们得出求 的似然函数为：

4.5 对数似然

由于上述的累乘的方法不太方便我们去求解 ，我们可以转换成对数似然，将以上公式放到对数中，然后就可以转换成一个加法运算。取对数以后会改变结果值，但不会改变结果的大小顺序。我们只关心等于什么的时候，似然函数有最大值，不用管最大值是多少，即，不是求极值而是求极值点。注：此处log的底数为e。

对数似然公式如下：

对以上公式化简得：