普通人穷极一生要怎么能跟得上天才的脚步？一以贯之的努力，不可懈怠的人生，就算开局坏到极点的人，也有无限可能。普通人如何做到天才那样，获得成功？一以贯之的努力，不可懈怠的人生，每天的微小积累会决定最终结果，这就是答案。

——《天才基本法》

本文先讨论红蓝球问题和三门问题，接下来谈谈贝叶斯定理，最后讨论辛普森*妻案的条件概率问题。

热播电视剧《天才基本法》第4集，主角团参加小学奥数夏令营选拔赛，最后一题是一道概率题。

有三个完全相同的盒子，一个盒子里面装了两个红球，一个盒子里面装了两个蓝球，一个盒子里面装的是一个蓝球、一个红球。

从三个盒子中随机选择了一个盒子，从里面拿出了一个球，发现是红色的，问这个盒子里剩下的那个球是红色的概率有多大？

刚开始林朝夕的思路是，盒子里有红球，排除了两个都是蓝球的盒子，所以只能是两个红球的盒子或者一红一蓝的盒子，所以概率是1/2。这种思路通常也是大多数人的直觉。

但后来，林朝夕意识到双红盒子和红蓝盒子的概率不是等可能的。

用列举法解题，从三个盒子中摸出一个球，有6个摸球可能，其中摸出红球有3种可能，另外一个球也是红球有2种可能，所以最后的概率应该是2/3。

电视剧里展示了章亮的解题思路，即大学生的解法。

解:设摸出第一个球为红球是事件A，盒子里剩下的球是红球是事件B，求P(B|A)是多少？

P(AB)=⅓，P(AB)是指事件A和事件B都发生的概率，显然是⅓。因为在3个盒子中，只有选中了红红盒子，才会发生事件A和事件B。

接下来计算事件A发生的概率:

P(A)=⅓·1 ⅓·0 ⅓·½

=½

题目问的是当事件A发生时，事件B发生的概率是多少？这是一个条件概率问题，把上面的计算结果套公式就算出来了。

条件概率公式有两个，请看下图:

条件概率公式

套公式的计算过程请看下图:

红蓝球问题的答案

正确答案是三分之二。

电视剧里林朝夕用小学生解法求出了正确答案。曹奂东的b站视频解说讲得非常好，他说，把红球编号，红红盒子里的两个红球编号为1和2，红蓝盒子里的红球编号为3，于是问题转化为下面的同构问题了:

有三个红球，摸到1号或2号的概率是多少？

摸到1号代表成功，摸到2号代表成功，摸到3号代表失败。条件概率问题其实就是限制了你的选择范围，缩小了包围圈，然后再让你计算需要求的概率。

问题转化以后，现在答案就像水晶一样透明，当然是三分之二啦。你摸三次，成功两次，失败一次，很容易理解。

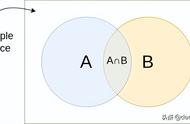
曹奂东还提到了可以用文恩图解决这个概率问题。

从考场出来后，电视剧里的对话还提到了三门问题。

三门问题（Monty Hall problem）亦称为蒙提霍尔问题、蒙特霍问题或蒙提霍尔悖论，大致出自美国的电视游戏节目Let's Make a Deal。问题名字来自该节目的主持人蒙提·霍尔（Monty Hall）。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆劳斯莱斯汽车，选中后面有车的那扇门可赢得该汽车，另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，节目主持人开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门是否会增加参赛者赢得汽车的机率。如果严格按照上述的条件，那么答案是会。不换门的话，赢得汽车的几率是1/3。换门的话，赢得汽车的几率是2/3。

由于该问题的答案十分违反普通人的直觉，在多年以前曾引起一阵热烈的讨论。

这个问题的答案很容易验证。你可以在纸上做实验，把三个门标号为1，2，3，再任意假定一个编号藏着劳斯莱斯。你连续猜3次，每次猜不同的门。根据实验结果就可以计算出换门后的成功率由⅓上升到了三分之二。

你有没有做过这样的噩梦：马上就要期末考试了，你突然发现有一门课你从来没有上过，试卷的内容你一点儿也看不懂？这是学生的噩梦。

而教授的噩梦与学生的噩梦正好相反，教授会梦见自己站在讲台上准备讲课，却突然发现要讲的内容自己一点儿也不记得了。

每次上概率课的时候，我就好像生活在这样的噩梦里。我自己做学生的时候从来没上过概率课，所以对我来说，给学生们上概率课既恐怖又有趣，就好像是在游乐园游玩时进“鬼屋”一样。

概率课上最能让我心跳过速的内容是条件概率：在发生事件B的前提下，发生事件A的条件概率是多少（即已知事件B发生，在此条件下事件A发生的概率是多少）？

这个概念非常复杂，很容易就会把B发生的前提下A发生的条件概率，与A发生的前提下B发生的条件概率相混淆。这两个概念当然是不一样的，但是，需要集中注意力保持头脑清醒，才能搞清楚它们之间的区别。

在举例之前，我们先考虑下面这个问题。你打算外出度假一周，出发之前，你请一个粗心的朋友帮你给一棵“生病”的植物浇水。如果不浇水，这棵植物有90%的概率会死掉。但即使是用心浇水，这棵植物也有20%的概率会死掉。根据你的判断，这个粗心的朋友忘记浇水的概率是30%。

以上是本题的条件，本题的问题如下：（a）你回来时，这棵植物还活着的概率是多大？

（b）如果你回来时发现植物已经死了，请问你的朋友没有浇水的概率是多大？

（c）如果你的朋友没有给植物浇水，你回来时发现植物死了的概率是多大？

虽然（b）问题和（c）问题听起来差不多，但是这两个问题是不一样的，答案当然也不一样。实际上，题目的条件已经告诉我们，“如果不给植物浇水，这棵植物有90%的概率会死掉”，所以问题（c）的答案是90%。

但是，怎样利用这些条件求解出（a）和（b）问题的答案呢？

因为我对概率不大熟悉，所以一开始教这门课的时候，我主要追求稳妥：什么都按照书本来，像上面这种题目我就直接套用书本上的公式来解答。

但是渐渐地，我发现有些学生不用贝叶斯定理也能解出这类题目。为了绕过繁杂的贝叶斯定理，这些聪明的同学用一种与贝叶斯定理的原理相同但却更加简单明了的方法来解答这类题目。

时光飞逝，我给一届又一届的学生讲授概率课。在这些聪明学生的启发下，我慢慢地发现了一套理解条件概率的更好的办法。

贝叶斯定理看上去很令人迷惑，而这些学生教我的方法则完全顺应人的直觉。这个方法的窍门就是，不要去想抽象的概率、机会、百分比之类的概念，而是直接考虑事情发生的次数（显然，这是一种更为自然的频率计算法，也可称为事件的“自然频率”）。只要转变思路，一切就都豁然开朗了。

就职于柏林马克思·普朗克人类发展研究所的认知心理学家捷尔德·盖格瑞泽写了一本非常有意思的书，书名为《风险的计算》。

在这本书中，盖格瑞泽举出了很多他在研究中发现的人类对风险和不确定性的误判和错误计算。算错概率的例子遍及各个领域：从艾滋病治疗到脱氧核糖核酸（DNA）指纹图谱的识别。

虽然我们计算概率的时候常常错得离谱儿，但是这位仁慈的心理学家并没有责骂我们的愚蠢，也没有哀叹人类的脆弱，他只是耐心地告诉我们怎样才能减少这类错误。

盖格瑞泽的方法和我的学生们发明的方法差不多，那就是，当面对条件概率问题的时候，不使用抽象的概率和百分比，而是依赖最自然、最原始的计数方法：计算事件发生的次数（自然频率）。

在其中一项研究中，盖格瑞泽和他的同事请德国和美国的医生们来解答这样一个问题：

如果一位妇女的乳房X射线检查结果呈阳性，但是这位妇女又属于乳腺癌发病风险较低的人群（年龄在40~50岁，无家族乳腺癌病史，本人无乳腺癌症状），那么她罹患乳腺癌的概率到底有多大？

为了把问题进一步具体化，盖格瑞泽给受访的医生们提供了如下信息：一是这个人群中乳癌的发病率，二是乳房X射线检查的灵敏度和阴性被误判为阳性的概率。

这些信息都是以概率和百分比的形式给出的，具体数据如下：

在年龄为40~50岁、无家族乳腺癌病史、本人无乳腺癌症状的妇女中，乳腺癌发病率是0.8%。如果一位妇女确实患有乳腺癌，那么乳房X射线检查呈阳性的概率是90%。如果一位妇女没有患上乳腺癌，但乳房X射线检查结果呈阳性的概率为7%。

现在，有一位妇女，她属于乳腺癌发病风险较低的人群，但是她的乳房X射线检查结果呈阳性，请问她实际患有乳腺癌的概率是多少？

盖格瑞泽询问的第一位医生是一所大学附属医院某部门的主任，对于乳腺癌的诊断，这位医生有着超过30年的专业经验。根据盖格瑞泽的描述，这位医生对上述问题的反应是这样的：我提出这个问题以后，这位医生显得很紧张，他很努力地想要算出正确的数值。在仔细研究过我给出的数据以后，这位医生判断，在乳房X射线检查结果呈阳性的前提下，这位妇女实际患有乳腺癌的概率是90%。

回答完这个问题以后，这位医生又立刻推翻了自己的答案，他紧张地说：“我肯定搞错了，我根本不会算。你应该去问我的女儿，她正在医学院读书。”

显然，这位医生很清楚自己的答案是错误的，但是他却不知道怎么才能算对。虽然他对这个问题冥思苦想了足有10分钟，但他却根本不清楚应该怎样使用概率。

同样的问题，盖格瑞泽又询问了24位德国医生，这些医生给出的答案五花八门。有8位医生认为，这位妇女实际患有乳腺癌的概率应该为10%或者更低；另有8个医生认为，这位妇女实际患有乳腺癌的概率是90%；剩下的8名医生认为，这位妇女实际患有乳腺癌的概率为50%~80%。

想象一下，如果你是一位病人，听到这些结果不一的诊断意见，你的心里会有多么痛苦。

那么，美国医生的表现又如何呢？85%的受访医生认为，该妇女罹患乳癌的概率应该约为75%。

其实，这道题的正确答案是9%。

为什么这位妇女实际患乳癌的概率这么低？盖格瑞泽指出，只要把题目的说法从概率和百分比“翻译”成事件发生的次数，这道题就会变得非常简单。

具体翻译如下：

在年龄为40~50岁、无家族乳腺癌病史、本人无乳腺癌症状的每1 000位妇女中，就会有8人罹患乳腺癌。这8个人中有7个人的乳房X射线检查结果呈阳性。在没有患上乳腺癌的992人中，大约有70人的乳房X射线检查结果会错误地显示为阳性。现在有一个乳房X射线检查结果呈阳性的妇女，请问她实际患有乳腺癌的概率是多少？

非常简单。1 000人中检查结果呈阳性的一共有7＋70=77个人。这77个人中，只有7个人确实是乳腺癌患者，剩下的70人并没有患上乳腺癌。所以，在检查结果呈阳性的前提下，实际患有乳腺癌的概率是7除以77，也就是1/11或者约9%。

在上面的计算中，我们做了两处简化。

第一，我们把所有小数四舍五入为整数。比如，“这8个人中有7个人的乳房X射线检查结果呈阳性”。准确地说，8个患乳腺癌的人乳房X射线检查结果呈阳性的概率为90%，也就是说有8×0.9=7.2个人乳房X射线的检查结果呈阳性。此处，我们把7.2直接四舍五入为7，虽然精确度有所下降，但是整数会比小数更清楚易懂。

第二，我们假设实际情况和统计数据是完全相符的。比如，低风险人群的乳腺癌发病率是0.8%，那么假设1 000人样本中正好有8个人患病。

现实中，情况往往不是这样，你抛1 000次硬币，不一定正好有500次的结果是正面朝上的。但是，我们需要假设样本完全服从统计数据的分布规律，否则我们就没办法计算了。

不得不承认，这个方法在逻辑上并不是很严密，所以，任何一本概率学教科书都不会采用这种方法。

但是，与复杂的贝叶斯定理相比，我们的这种方法既简单又清楚，光这两个优点其实已经足够了。

作为上述实验的对照，盖格瑞泽又找了另外24位医生，向他们提出同样的问题，只不过这次的数据不是以概率和百分比的形式给出，而是以事件发生的自然频率的形式给出（即直接给出翻译过后的题目）。结果是，几乎所有受访医生都给出了正确的答案（或者答案与正确答案很接近）。

把概率从百分比简化成事件发生次数，确实使问题解决起来容易许多，但是条件概率仍然是一个比较复杂的内容。有时候，我们甚至连问题都问错了；还有的时候，我们算出了正确的结果，却又被结果所误导，给出了错误的解释。

在1994~1995年辛普森*妻案的庭审过程中，控方和辩方都犯了这类错误。在法庭上，双方律师都用错误的条件概率误导过陪审团。

在庭审的最初10天内，控方举出了无数证据说明辛普森常对前妻妮可尔·布朗实施家庭暴力。这几乎是控方这10天诉讼的唯一主题。

控方声称，辛普森曾多次殴打前妻，把她往墙上推，甚至当众指着妮可尔对围观群众说：“看，这是属于我的东西！”但问题是，辛普森虐待前妻与他有没有谋*她有什么关系呢？

控方的观点是，长期对前妻实施家庭暴力说明辛普森有谋*前妻的动机。按照控方自己的说法就是：“一个巴掌可能就是谋*的前兆。”

而辩方律师阿兰·德尔绍维茨则反驳说，就算这些家暴事件全部属实，也和谋*没有必然关系，所以不应该被采纳。

阿兰·德尔绍维茨后来写道：“殴打配偶的男性中，只有非常少的人最后真的会谋*配偶，这个概率低于1/2500。如果庭审需要，我们可以轻松地明确证实这一点。”

实际上，不管是控方还是辩方，都在诱导陪审团考虑这样一个条件概率：在已知丈夫曾经殴打妻子的前提下，丈夫谋*妻子的概率是多少。

但是，正如统计学家I·J·古德所指出的那样，这个问题其实是错误的，陪审团应该考虑的并不是这个条件概率。正确的问题应该是：在已知丈夫曾经殴打妻子，并且妻子确实死于谋*的双重前提下，丈夫谋*妻子的概率是多少。

经过调查和计算，这个条件概率远远高于1/2500。

为什么呢？让我们再次使用自然频率法，把概率和百分比转换成事件发生的次数。想象我们的样本是100 000个被丈夫殴打过的妇女。假设阿兰·德尔绍维茨的数据属实，那么这其中大概有40个妇女最终会被丈夫谋*（100 000×1/2 500 = 40）。

我们再假设，另外还有3个妇女被丈夫以外的人谋*了（这是根据美国联邦调查局于1992年发布的女性被谋*的数据算出来的）。

也就是说，被谋*的43位女性中，有40个妇女是被对她们实施家暴行为的丈夫*掉的。

因此，在已知丈夫曾经殴打妻子，并且妻子确实被人谋*的双重前提下，丈夫谋*妻子的概率高达93%！

当然，这个概率并不是辛普森*妻的概率。辛普森是本案凶手的概率到底有多大，还取决于很多其他的证据（包括对他有利的证据和对他不利的证据）。

比如，辩方称警方曾陷害过辛普森，控方则称凶手的鞋印、手套、DNA都与辛普森相吻合等。但是，这些证据影响你对最终判决看法的概率又是多少呢？我想这个概率可能是零。

以上第三和第四两个单元的内容来自美国应用数学家斯托加茨的《x的奇幻之旅》第23章。读了以后，我们明白提正确的问题是何等重要。

电视剧《天才基本法》里的主角林朝夕两次用贝叶斯定理和Python进行数学建模，还提到了先验概率和后验概率。第一次主力是裴之，林朝夕协助，第二次数学建模大赛的主力是林朝夕，裴之协助。

让普通人理解复杂的贝叶斯定理很难，阅读前面两个单元的书摘其实对普通人帮助更大，也更轻松。

前面我们已经介绍了条件概率公式，很自然就能够推导出乘法公式:

P(AB)=P(A|B)P(B)

=P(B|A)P(A)

我们把条件概率公式，乘法公式，全概率公式等组合起来，就能够得到贝叶斯定理:

贝叶斯公式(引自《数学辞海》第一卷)

托马斯·贝叶斯是18世纪的英国牧师。他原本准备计算神存在的概率，结果发现了这个贝叶斯公式。然而这个公式在贝叶斯生前并没有公布，而是过半世纪之后，法国数学家皮埃尔-西蒙·拉普拉斯在一本关于概率论的书中介绍了这个公式。此后，这个公式就为大家熟知了。

关于妇女接受乳腺癌检查的例子，需要指出一个数学角度的说明。用数学的概率论观点看问题，妇女接受乳腺癌检查是有意义的:

在接受检查前，确诊的概率是0.8%；在接受检查后阳性，概率上升到9%；如果再一次接受检查，还是阳性，概率就上升到58%了。

运用贝叶斯定理，每次获取新的信息后都知道如何修改概率。从数学的角度体现出学习“经验”。

所谓进步，就是积累经验，获取更为正确的知识。每当遇到新信息，我们需要拥有能够改变之前判断的勇气和沉稳的内心。这也是我们从贝叶斯定理中学到的。

查阅资料可以让我们获得需要的知识，所谓书到用时方恨少。

接下来请看《数学辞海》第一卷关于概率论的一些相关知识点。