理论上，只要古人口袋里的 石子 足够多，就可以 记录任意 大的数字。不仅如此，石子还具有天然的计算能力，例如：

• 将 2 个石子 和 3 个石子放在 一起，自然就得到了 2 3=5 个 石子；
• 将 石子 排列成 2 行 3 列，自然就 得到了 2×3=6 个 石子。

石子甚至，还可以用来证明一些代数定理，例如：

注：这种对应石子可摆基本几何图形的数，被称为形数，它是毕达哥拉斯学派的研究对象之一。关于形数，有机会，再详细给大家介绍。

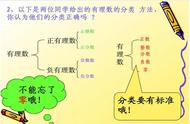
我们有理由猜想：围棋盘最早就是用来计算的“计算盘”，而黑白石子分别表示正负整数。

当然，石头还是太沉，不方便携带，于是我们的祖先又用短棍代替了石子，这就是算筹。

理论上，短棍是一维的线，石子是零维的点，因此，前者可以比后者表示更多信息，实际上也是如此：

我们的祖先用 1、2、3、4、5 根 纵放的短棍 分别表示数字 1、2、3、4、5， 这与 石子 的区别不大，但之后 用 1 根横着摆放的短棍 分别加上 1、2、3、4、根 纵放的短棍 来表示数字6、7、8、9，可就比 石子表示 “节省用料” 了。

接下来的 10 和 1 的表示一样，只不过短棍摆放位置向左移1位，之后只要在右边留出的空位上分别摆放1到9对应的短棍，就表示了数字 11 到 19；同时，再将左边的1分别替换为2到9，就可以表示20到99的所有数字了。

再接下来的 100 又复归 1 的表示，只不过短棍摆放位置向左移2位，之后 ... ...

... ...

从右向左数：

• 第1位称为个位，其上的每个数字就是它原本的值；
• 第2位称为十位，其上的每个数字是它原值的10倍；
• 第3位称为百位，其上的每个数字是它原值的100倍；
• 第4位称为千位，其上的每个数字是它原值的1000倍；
• 第5位称为万位，其上的每个数字是它原值的10000倍；
• ... ...

这种靠位置区分数字值的方法，叫做 位值制，是由中国老祖宗率先创造，并一直沿用到现在的阿拉伯数字中。

大家有没有发现：1到5的短棍摆放，和竖起的手指是多么相似，也许 短棍 本身就是 十根手指 不够用的 直接 替代品，中间不经过 石子。

在算筹的计数方法中，一个空位表示的数字0，聪明的读者会注意到，这存在一个问题：

若没有上下文数字定位参考，1根单独纵置的短棍，很难区分它是1还是10。

为了解决这个问题，老祖宗让所有处于处于10位的短棍，旋转90°，这样就得到了另外一种横置的摆放方式：