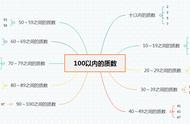
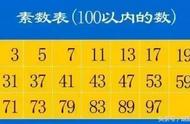
密密麻麻的趴在栅栏上的周期蝉
数学之美,无处不在。就以素数这个特性而言,一方面,人类在计算机的加密算法上,运用到了素数分布的特性;另一方面,大自然按照既定的规律自然运行,却也产生素数周期的特性,素数周期的生物产生了最大的适应性,实在令人惊叹。这让人联想到,诸如蕴含费波那契数列的松果,具有分形结构的山川河流(传送门),与其说这是自然界的神工鬼斧,倒不如说,这是数学规律幕后主使的结果。

松果顺时针8环,逆时针13环,这正是费波那契数列当中的数字
数学家对素数干了什么?
素数如同数字的原子一样,是构造其他数字的基石。自然数是无限个,那么作为基石的素数到底有多少个呢?
这个问题在2300多年前得到了解答:素数有无穷多个。古希腊数学家欧几里得在《几何原本》中给出了简洁漂亮的证明。
虽然素数有无穷多个,但要发现和验证大素数却不容易,这就是素数的秘密。有多不容易呢?

我们可以很快地把50以内的素数列举出来:
2,3,5,7,11,13,17,19,23,29,31,37,41,43,47……
它们看起来很密集,但随着素数越大,它们之间的距离渐渐变长。
重要的是,它们的分布距离是不均等的。要找到一个大的素数,往往需要巨量的计算,要分解和验证它也是这样。为了掌握素数的规律,数学家绞尽脑汁。
其中,有两个关于素数的著名猜想:
孪生素数猜想:存在无限多组之差为2的素数对。哥德巴赫猜想:所有的偶数都可以表示为两个素数之和。
这两个猜想在数学史上非常有名,千百年来许多数学家梦寐以求希望亲手攻克的难题。可喜的是,在最近的100年,这两个猜想得到了重大的突破。

张益唐教授
其中,中国数学家张益唐在2012年成功地证明了存在无数对孪生素数,而且其中每一对中的两个素数之差,不超过7000万。虽然只有把7000万降到2才能最终证明孪生素数猜想,但他突破性地把孪生素数的距离,从无限变成了有限。
在张益唐取得这一突破之后,不少学者尝试用他的方法缩小间隔,进一步拉近了与最终解决孪生素数猜想的距离。在2014年2月, 7000万已被缩小至246。
另一方面,中国数学家陈景润在1966年成功证明了“1 2”的成立,距离哥德巴赫猜想“1 1”的成立仅一步之遥。
这里引入一个概念叫殆素数,殆素数是素因子个数不多的正整数。假设N是偶数,虽然目前不能证明N是两个素数之和,但足以证明它能够写成两个殆素数的和,即N=A B,其中A和B的素因子个数都不太多,譬如说素因子个数不超过10。我们可以用“a b”来表示如下命题:每个大偶数N都可表为A B,其中A和B的素因子个数分别不超过a和b。显然,哥德巴赫猜想就可以写成"1 1"。在这一方向上的进展都是用所谓的筛法得到的。自从1920年挪威数学家布朗(Brun)证明了“9 9”以来,这个公式在各大数学家手上不断进行简化,在1966年由我国数学家陈景润证明了“1 2”。
素数寻找计划——GIMPS
素数当中,有一类素数非常特别,形如2p-1,17世纪法国数学家马林·梅森对它进行了深入研究。为了纪念梅森的贡献,学界把这种数称之为梅森数,如果梅森数为素数,则称之为梅森素数。