前言:
作为一枚初中数学老师,我深知学生时间太宝贵,从而上课亦或是学生问题时,往往三下五除二,技巧性概括,技巧性总结,技巧性解答,从而皆大欢喜,学生收获了答案,我节约了时间,慢慢,渐成习惯!后来,我拜读过许多优秀老师的几何解题心得,也听过大量的几何视频讲解,简单如:角平分线、倍长中线、将军饮马等等,稍复杂如:胡不归,阿氏圆,费马点等等,无一例外,讲的是精彩纷呈。而对于这种种模型背后的解释却鲜少有人提及,或许教育者本身能够理解,而对于被动听者的学生又能理解多少呢?基于此,特“旁征博引”,发出一点点我的浅解!希望各位老师、家长、同学,在讲解或学习几何技巧的背后也能稍作停留,能多些解释说明!
从全国各地每年的中考试卷里都会出现考查几何的证明和计算问题,在解答试题过程中,我们发现当题设条件不够,必须添加辅助线,把分散条件集中,建立已知和未知的桥梁,结合学过的知识,采用一定的数学方法,把问题转化为自己能解决的问题。学会添加辅助线技巧,是培养学生科学思维、科学探究的重要途径。所以希望大家学深学透添加辅助线的技巧和方法。
一、以基本图形为切入点研究添加辅助线的技巧策略
1.三角形问题
方法1:有关三角形中线的题目,常将中线加倍。含有中点的题目,常常利用三角形的中位线,通过这种方法,把要证的结论恰当的转移,很容易地解决问题。
方法2:含有平分线的题目,常以角平分线为对称轴,利用角平分线的性质和题中的条件,构造出全等三角形,从而利用全等三角形的知识解决问题。
方法3:结论是两线段相等的题目常画辅助线构成全等三角形,或利用关于平分线段的一些定理。
方法4:结论是一条线段与另一条线段之和等于第三条线段这类题目,常采用截长法或补短法,所谓截长法就是把第三条线段分成两部分,证其中的一部分等于第一条线段,而另一部分等于第二条线段。
2.平行四边形问题平行四边形(包括矩形、正方形、菱形)的两组对边、对角和对角线都具有某些相同性质,所以在添辅助线方法上也有共同之处,目的都是造就线段的平行、垂直,构成三角形的全等、相似,把平行四边形问题转化成常见的三角形、正方形等问题处理,其常用方法有下列几种,举例简解如下:
(1)连对角线或平移对角线;
(2)过顶点作对边的垂线构造直角三角形;
(3)连接对角线交点与一边中点,或过对角线交点作一边的平行线,构造线段平行或中位线;
(4)连接顶点与对边上一点的线段或延长这条线段,构造三角形相似或等积三角形;
(5)过顶点作对角线的垂线,构成线段平行或三角形全等;
3.梯形问题梯形是一种特殊的四边形。它是平行四边形、三角形知识的综合,通过添加适当的辅助线将梯形问题化归为平行四边形问题或三角形问题来解决。辅助线的添加成为问题解决的桥梁,梯形中常用到的辅助线有:
(1)在梯形内部平移一腰;
(2)梯形外平移一腰;
(3)梯形内平移两腰;
(4)延长两腰;
(5)过梯形上底的两端点向下底作高;
(6)平移对角线;
(7)连接梯形一顶点及一腰的中点;
(8)过一腰的中点作另一腰的平行线;
(9)作中位线。
当然在梯形的有关证明和计算中,添加的辅助线并不一定是固定不变的、单一的。通过辅助线这座桥梁,将梯形问题化归为平行四边形问题或三角形问题来解决,这是解决问题的关键。
4.圆中常用辅助线的添法在平面几何中,解决与圆有关的问题时,常常需要添加适当的辅助线,架起题设和结论间的桥梁,从而使问题化难为易,顺其自然地得到解决,因此,灵活掌握作辅助线的一般规律和常见方法,对提高学生分析问题和解决问题的能力是大有帮助的。
(1)见弦作弦心距。有关弦的问题,常作其弦心距(有时还须作出相应的半径),通过垂径平分定理,来沟通题设与结论间的联系。
(2)见直径作圆周角。在题目中若已知圆的直径,一般是作直径所对的圆周角,利用"直径所对的圆周角是直角"这一特征来证明问题。
(3)见切线作半径。命题的条件中含有圆的切线,往往是连结过切点的半径,利用"切线与半径垂直"这一性质来证明问题。
(4)两圆相切作公切线。对两圆相切的问题,一般是经过切点作两圆的公切线或作它们的连心线,通过公切线可以找到与圆有关的角的关系。
(5)两圆相交作公共弦。对两圆相交的问题,通常是作出公共弦,通过公共弦既可把两圆的弦联系起来,又可以把两圆中的圆周角或圆心角联系起来。
二、添加辅助线的重要方法总结
1.中点、中位线,延线,平行线。如遇条件中有中点,中线、中位线等,那么过中点,延长中线或中位线作辅助线,使延长的某一段等于中线或中位线;另一种辅助线是过中点作已知边或线段的平行线,以达到应用某个定理或造成全等的目的。
2.垂线、分角线,翻转全等。如遇条件中,有垂线或角的平分线,可以把图形按轴对称的方法,并借助其他条件,而旋转180度,得到全等形,这时辅助线的做法就会应运而生。其对称轴是垂线或角的平分线。
3.边边若相等,旋转。如遇条件中有多边形的两边相等或两角相等,有时边角互相配合,然后把图形旋转一定的角度,就可以得到全等形,这时辅助线的做法仍会应运而生。其对称中心,因题而异,有时没有中心。故可分“有心”和“无心”旋转两种。
4.造角、平移、相似,和、差、积、商。如遇条件中有多边形的两边相等或两角相等,欲证线段或角的和差积商,往往与相似形有关。在制造两个三角形相似时,一般地,有两种方法:第一,造一个辅助角等于已知角;第二,是把三角形中的某一线段进行平移。故作歌诀:“造角、平、相似,和差积商见”
5.两圆若相交,连心公共弦。如果条件中出现两圆相交,那么辅助线往往是连心线或公共弦。
6.两圆相切、离,连心,公切线。如条件中出现两圆相切(外切,内切),或相离(内含、外离),那么,辅助线往往是连心线或内外公切线。
7.切线连直径,直角与半圆。如果条件中出现圆的切线,那么辅助线是过切点的直径或半径使出现直角;相反,条件中是圆的直径,半径,那么辅助线是过直径(或半径)端点的切线。即切线与直径互为辅助线。如果条件中有直角三角形,那么作辅助线往往是斜边为直径作辅助圆,或半圆;相反,条件中有半圆,那么在直径上找圆周角——直角为辅助线。即直角与半圆互为辅助线。
8.弧、弦、弦心距;平行、等距、弦。如遇弧,则弧上的弦是辅助线;如遇弦,则弦心距为辅助线。如遇平行线,则平行线间的距离相等,距离为辅助线;反之,亦成立。如遇平行弦,则平行线间的距离相等,所夹的弦亦相等,距离和所夹的弦都可视为辅助线,反之,亦成立。有时,圆周角,弦切角,圆心角,圆内角和圆外角也存在因果关系互相联想作辅助线。
9.面积找底高,多边变三边。如遇求面积,(在条件和结论中出现线段的平方、乘积,仍可视为求面积),往往作底或高为辅助线,而两三角形的等底或等高是思考的关键。如遇多边形,想法割补成三角形;反之,亦成立。
三、初中几何常见辅助线作法歌诀
人说几何很困难,难点就在辅助线。
辅助线,如何添?把握定理和概念。
还要刻苦加钻研,找出规律凭经验。
辅助线,是虚线,画图注意勿改变。
假如图形较分散,对称旋转去实验。
基本作图很关键,平时掌握要熟练。
解题还要多心眼,经常总结方法显。
切勿盲目乱添线,方法灵活应多变。
分析综合方法选,困难再多也会减。
虚心勤学加苦练,成绩上升成直线。
三角形图中有角平分线,
可向两边作垂线。
也可将图对折看,
对称以后关系现。
角平分线平行线,等腰三角形来添。
角平分线加垂线,三线合一试试看。
线段垂直平分线,常向两端把线连。
要证线段倍与半,延长缩短可试验。
三角形中两中点,连接则成中位线。
三角形中有中线,延长中线等中线。
四边形平行四边形出现,
对称中心等分点。
梯形里面作高线,平移一腰试试看。
平行移动对角线,补成三角形常见。
证相似,比线段,添线平行成习惯。
等积式子比例换,寻找线段很关键。
直接证明有困难,等量代换少麻烦。
斜边上面作高线,比例中项一大片。
圆半径与弦长计算,弦心距来中间站。
圆上若有一切线,切点圆心半径连。
切线长度的计算,勾股定理最方便。
要想证明是切线,半径垂线仔细辨。
是直径,成半圆,想成直角径连弦。
弧有中点圆心连,垂径定理要记全。
圆周角边两条弦,直径和弦端点连。
弦切角边切线弦,同弧对角等找完。
要想作个外接圆,各边作出中垂线。
还要作个内接圆,内角平分线梦圆。
如果遇到相交圆,不要忘作公共弦。
内外相切的两圆,经过切点公切线。
若是添上连心线,切点肯定在上面。
要作等角添个圆,证明题目少困难。
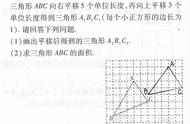
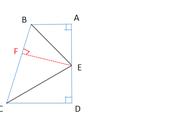
专题训练