康托尔
欧氏几何的五大公理1、任意两个点可以通过一条直线连接。
2、任意线段能无限延长成一条直线。
3、给定任意线段,可以以其一个端点作为圆心,该线段作为半径作一个圆。
4、所有直角都全等。
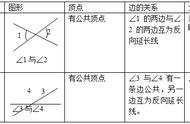
5、如果一条直线与两条直线相交,使得一侧的内角不都是直角,则将这两条直线延长,它们在内角不都是直角的直线一侧相交。即若∠1 ∠2<180°,将a,b充分延长,它们必定相交。

欧氏几何中的第五公理,一直在困惑着数学家们,不是由于它的正确性,而是由于它的表达方式。第五公理缺少了其他公理的简洁性,令人不知所措,欧几里得本人也不喜欢,直到所有不经过它的定理都被证明出来之后,欧几里得才不得以提出来。
在数论和其他任何比较完善的数学理论中,所谓的公理都是解释性的,而非基础性的。——哥德尔

哥德尔
平行公理问题公理的实质在于符合经验而并非其不证自明——克吕格尔
第五公理又称为“平行公理”,为了避免公理的冗长,数学家们做了两种不同类型的尝试,一种是用更加自明的命题来代替平行公理。另一种是试图从欧几里得的其他公理中推导出平行公理,将其变为定理,使其不容置疑。

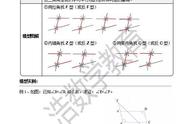
最为人知晓的替代公理是,普莱费尔提出的平行公理的说法:给定一条直线,通过此直线外的任何一点P,有且只有一条直线与之平行。另外还有“三角形内角和为两直角”、“存在两个相似但不全等的三角形”、“所有三角形都有外接圆”、“存在一对等距的直线”等等。所有的替代公理似乎都比欧几里得的要简单,但进一步研究证明,它们并不比欧几里得的叙述更令人满意。