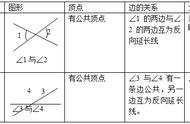
在尝试用其他公理推出平行公理的努力中,最有意义的是萨谢利的工作。他提出了各种假设,首先假定过P点没有与l平行的直线,则由此公理和欧几里得其他公理,萨谢利认为可以推出矛盾。接着又假设过P点至少有2条直线p和q,不管如何延伸总不与l相交,然后他得到一个奇怪的结论,于是萨谢利认为这也是矛盾的。由此萨谢利得出结论:平行公理是其他公理的推论。其实后来的数学家发现其中并没有真正的矛盾,因此平行公理的问题依然存在。

萨谢利
平行公理问题的徒劳无功,让数学家们终于意识到欧几里得的平行公理中的深刻意义。
非欧几何的诞生任何较大的数学成果,都不会只是个人的工作。充其量,某些决定性步骤或证明可以归功于个人。——克莱因
渐渐地数学家们终于意识到平行公理不能由其它公理推出,平行公理是建立欧氏几何所必需的条件。既然平行公理是独立的,逻辑上讲,可以假设一个与此矛盾的命题,从而作为新的公理,是不是可以导出新的几何?

克莱因
数学家罗巴切夫斯基是第一个真正意义上放弃欧几里得平行公理的人,他提出了自己的假设:给定一条直线,通过此直线外的P点允许有无限多条平行线。

若角A等于90°则得到欧几里得的平行公理;
若A为锐角,随着距离a趋于0,则角A增大趋于90°,当a趋于无穷大,则角A减小且趋于0°。于是,三角形的内角和总是小于180°,且随着三角形面积的减小而趋近于180°,且两个相似三角形必定全等。