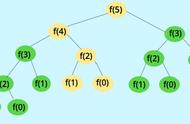
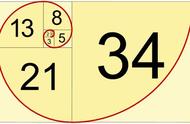
斐波那契数列(Fibonacci sequence)，又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入，故又称为“兔子数列”，指的是这样一个数列：1、1、2、3、5、8、13、21、34、……在数学上，斐波纳契数列以如下被以递推的方法定义：F(1)=1，F(2)=1, F(3)=2,F(n)=F(n-1) F(n-2)(n>=4，n∈N*)在现代物理、准晶体结构、化学等领域，斐波纳契数列都有直接的应用，为此，美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。

艾略特波浪理论的基础——斐波那契数列在波浪理论中应用的周期是以斐波那契数列为基础的，斐波那契数列是以最简单的数字123作为基本数列的，把这个简单数列的后两位数字不断相加，如1 2=3，2 3=5，3 5=8，5 8=13 ，8 13=21 等等，从而得出斐波那契数列3、5、8、13、21、34、55、89、144……以至无穷。

神奇数列是指3、5、8、13、21、34、55、89.....等数字构成的数列，称为“斐波那契神奇数列”，其特点是：神奇数列内，一个数字同其后一个数字的比值，大致接近于0.618的黄金分割比;而第三个数字，总是前两个数字之和。

随着数列项数的增加，每一个数字与后一个数字的比值无限接近于0.618。如2/3=0.666，5/8=0.625，21/34=0.6176，34/55=0.6181，55/89=0.6179……

在股市里面，运用神奇数列，可以更好地预测和把握变盘的机会、把握波段转点的出现机会。

例如，

2001年6月14日见顶2245点之后的88个交易日(同89的神奇数字仅误差一天)在10月22日见底1514点;

10月22日开始反弹到10月24日波段性高点1744点即告回落，期间只有3个交易日，恰为斐波那契神奇数字;

10月22日开始的反弹延续到12月5日，见到波段性高点1776点，期间共有33个交易日(同34的神奇数字误差一天);

10月24日波段反弹的最高点1744点回落到11月8日波段最低点1550点，期间共有12个交易日(同13的神奇数字误差一天);

11月8日波段最低点1550点，反弹到12月5日，见到波段性高点1776点，期间共有20个交易日(同21的神奇数字误差一天);

12月5日波段最高点1776点展开回落，到2002年元月23日波段性低点1346点，期间是33个交易日(同34的神奇数字误差1天);

而从元月23日1346点反弹到3月21日1693点波段反弹的最高点，期间共32个交易日(同34的神奇数字误差2天)。

而从3月4日1494点波段性低点到3月21日1693点波段反弹的最高点，期间共14个交易日(同13的神奇数字误差1天)

若本文对你有帮助，可关注公众号越声攻略(yslc688)，更多股票技术分析方法及操作技巧等你来学习!

(本资料仅供参考，不构成投资建议，投资时应审慎评估)