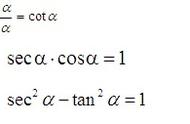最后就诱导公式在强调一下这个变，指的是正余弦互变，正余切互变。

第五、学法指导

我们在学了这些知识之后，针对他们的题型主要有如下三种：

第一、求值题型，已知一个角的一个三角函数值，求这个角的其他三角函数值；

这类问题，我们需要关注，角的象限或者终边位置已知，只有一解，角的象限或者终边需要判断；也或者，角的三角函数值含有字母，亦或是另一角的三角函数来表示，我们的解法是合理选择公式，一般思路是按照：“倒-平-倒-商-倒”的顺序很容易求解；在开平方的时候，应注意“±”的取舍，有时根据需要分类讨论。

第二、化简题型，目的是简化运算，要求项数尽量少，次数尽量低，尽量不含分母，尽量不带根号，尽量为数值。

以上是原则要求，需要关注的是，化简过程中，不要忽视三角函数的定义区间。

第三、证明题型，本质上是三角恒等式。

常用方法是：

1、从一边开始，证的另一边，由繁到简。

2、左右归一，证明左右两边都等于同一个式子。

3、凑合法，针对题设与结论间的差异，有针对性的变形，以消除差异，即化异为同。

4、比较法，即证明“左边-右边=0”,或者“左边÷右边=1”

5、分析法，从被证的等式出发，逐步探求使等式成立的充分条件，一直到已知条件或者明显的事实为止，就可以断定原等式成立。

常用的技巧：

1、负角化正角，大角化小角，化异为同，常用诱导公式；

2、切割化弦，弦切互化；

3、1的代换，1=sin²α cos²α=sec²α-tan²α=csc²α-cot²α=tanπ/4；

4、消元和降次；

5、sinα±cosα、sinαcosα，三个式子中，已知其中一个式子，可求其他两个式子，他隐藏一个条件是：弦的平方和为1。

以上是任意角的三角函数与诱导公式，熟练记忆透彻理解，就在这些口诀上和要点上，相信大家熟读以上，必定会为三角的学习奠定坚实的基础。加油！

就以上知识，大家不清楚的地方欢迎大家评论区留言，大黄必将竭尽全力为您解答。感谢！