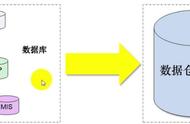
有一内壁光滑的闭合椭圆形管道,置于竖直平面内,MN是通过椭圆中心O点的水平线.已知一小球从M点出发,初速率为v₀,沿管MPN运动,到N点的速率为v₁,所需时间为t₁;若该小球仍由M点以初速率v₀出发,而沿管道MQN运动,到N点的速率为v₂,所需时间为t₂.则(A)
A. v₁=v₂,t₁>t₂
B. v₁<v₂,t₁>t₂
C.v₁=v₂,t₁<t₂
D.v₁<v₂,t₁<t₂

I卫星:卫星是指在围绕一颗行星轨道并按闭合轨道做周期性运行的天然天体,人造卫星一般亦可称为卫星。人造卫星是由人类建造,以太空飞行载具如火箭、航天飞机等发射到太空中,像天然卫星一样环绕地球或其它行星的装置。(不过,如果两个天体质量相当,它们所形成的系统一般称为双行星系统,而不是一颗行星和一颗天然卫星)

Ⅱ卫星轨道:可以是圆轨道(地心位于圆心),也可以是椭圆轨道(地心位于椭圆的一个焦点上),但轨道平面必过地心。
内容四:人造地球卫星的轨道:
人造卫星绕地球做匀速圆周运动时,由地球对它的万有引力提供向心力,地球对卫星的万有引力指向地心。而做匀速圆周运动的物体的向心力时刻指向它所做圆周运动的圆心。因此人造卫星绕地球做匀速圆周运动的圆心必与地心重合。这样就存在三类人造地球卫星轨道(如图所示):
①赤道轨道:卫星的轨道在赤道平面上,卫星始终处于赤道上方。
②极地轨道:卫星轨道平面与赤道平面垂直,卫星通过两极上空
③一般轨道:卫星轨道和赤道成一定的角度。
1.若轨道为椭圆,中心天体位于椭圆的焦点上,而不是中心上;
2.由面积定律得近日点速度大于远日点速度,且r₁v₁=r₂v₂;
3.圆和椭圆轨道卫星机械能都守恒;圆轨道的机械能为-GMm/2r,椭圆轨道的机械能为-GMm/2a.
4.卫星变轨问题,从低轨到高轨必须加速,从高轨到高低轨必须减速;
5.计算椭圆轨道周期,用开普勒第三定律;
6椭圆轨道的中心天体质量计算用开普勒第三定律。
例题:如图所示,

一天体m 绕另一天体M 运动,其运动轨迹为椭圆,天体M 处在椭圆其中一个焦点上,可认为静止不动.设OA 间的距离为rA,OB 间的距离为rB,天体m 运动到A 点和B 点的速度大小分别为vA和vB.
【卫星的椭圆运动】在地面附近发射飞行器,如果速度大于7.9km/s,而小于11.2km/s,它将沿椭圆轨道绕地球运行,地心就成为椭圆轨道的一个焦点.如果速度继续增大,达到或大于11.2km/s时(但需小于第三宇宙速度),它就会克服地球的引力,离开地球,成为绕太阳运动的一颗人造行星。